Question

A circle has end points (-2,1) and (8,3).

A) find its center

B) find the radius of the circle

C) find the equation of the circle

Answer 1

A) find its center = (3, 2)

B) find the radius of the circle = √104

C) find the equation of the circle = x² + y² - 6x - 4y -91 = 0

Explanation:

A)- The center must be the mid-points of (-2, 1) and (8, 3).

So, using the equation of mid-point,

`h=(x_(1)+x_(2))/(2)  and  k=(y_(1)+y_(2))/(2)`

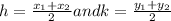
Here, (x₁, y₁) = (-2, 1) and (x₂, y₂) = (8, 3)

Putting these value in above equation. We get,

h = 3 and k = 2

Thus, Center = (h, k) = (3, 2)

B)- For finding the radius we have to find the distance between center and any of the end point.

Thus using Distance Formula,

`Distance=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`

`Radius =\sqrt{(8+2)^(2)+(3-1)^(2)}`

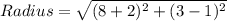
⇒ Radius = √104 = 2√26

C)- The equation of circle is determined by formula:

`(x-h)^(2)+(y - k)^(2) = r^(2)`

where (h, k ) is center of circle and

r is the radius of circle.

⇒ (x - 3)² + (y - 2)² = 104

⇒ x² + y² - 6x - 4y -91 = 0

which is the required equation of the circle.