Question

Time dilation: A missile moves with speed 6.5-10 m/s with respect to an observer on the ground. How long will it take the missile's clock to fall behind the ground observer's clock by 1 millisecond? Hint: use the binomial formula:(1+x)a1+ ax.

Answer 1

The time taken by missile's clock is
`4.6* 10^(6) s`

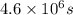
Solution:

As per the question:

Speed of the missile,
`v_(m = 6.5* 10^(3)) m/s`

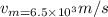
Now,

If 'T' be the time of the frame at rest then the dilated time as per the question is given as:

T' = T + 1

Now, using the time dilation eqn:

`T' = \frac{T}{\sqrt{1 + ((v_(m))/(c))^(2)}}`

`(T')/(T) = \frac{1}{\sqrt{1 + ((v_(m))/(c))^(2)}}`

`(T + 1)/(T) = \frac{1}{\sqrt{1 + ((v_(m))/(c))^(2)}}`

`1 + (1)/(T) = \frac{1}{\sqrt{1 + ((v_(m))/(c))^(2)}}`

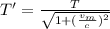
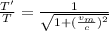
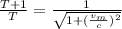
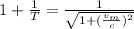
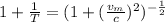`1 + (1)/(T) = (1 + ((v_(m))/(c))^(2))^{- (1)/(2)}` (1)

Using binomial theorem in the above eqn:

We know that:

`(1 + x)^(a) = 1 + ax`

Thus eqn (1) becomes:

`1 + (1)/(T) = 1 - (- 1)/(2).(v_(m)^(2))/(c^(2))`

`T = (2c^(2))/(v_(m)^(2))`

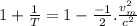
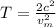
Now, putting appropriate values in the above eqn:

`T = (2(3* 10^(8))^(2))/((6.5* 10^(3))^(2))`

`T = 4.6* 10^(6) s`