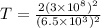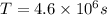Answer:
The time taken by missile's clock is
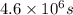
Solution:
As per the question:
Speed of the missile,
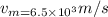
Now,
If 'T' be the time of the frame at rest then the dilated time as per the question is given as:
T' = T + 1
Now, using the time dilation eqn:
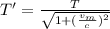
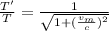
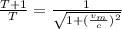
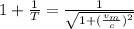
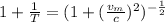 (1)
(1)
Using binomial theorem in the above eqn:
We know that:
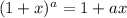
Thus eqn (1) becomes:
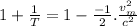
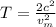
Now, putting appropriate values in the above eqn: