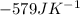Answer: The
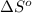 of the reaction is
of the reaction is
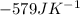
Step-by-step explanation:
Entropy change of the reaction is defined as the difference between the total entropy change of the products and the total entropy change of the reactants.
The equation representing entropy change of the reaction follows:
![\Delta S_(rxn)=\sum [n* \Delta S^o_(products)]-\sum [n* \Delta S^o_(reactants)]](https://img.qammunity.org/2020/formulas/chemistry/college/od07qddvxcc0son5an5fr21h8boi67g9v0.png)
For the given chemical equation:
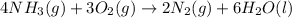
We are given:
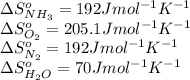
Putting values in above equation, we get:
![\Delta S^o_(rxn)=[(6* \Delta S^o_(H_2O))+(2* \Delta S^o_(N_2))]-[(4* \Delta S^o_(NH_3))+(3* \Delta S^o_(O_2))]](https://img.qammunity.org/2020/formulas/chemistry/college/myvp9gjn529j35ij8ny52hv3ss09qfkwsk.png)
![\Delta S^o_(rxn)=[(6* 70)+(2* 192)]-[(4* 192)+(3* 205.1)]=-579JK^(-1)](https://img.qammunity.org/2020/formulas/chemistry/college/txf2zknzwps82g3w2ubtbtbywopkuvhrqw.png)
Hence, the
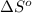 of the reaction is
of the reaction is