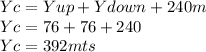Question

During launches, rockets often discard unneeded parts. A certain rocket starts from rest on the launch pad and accelerates upward at a steady 3.10 m/s^2. When it is 240 m above the launch pad, it discards a used fuel canister by simply disconnecting it. Once it is disconnected, the only force acting on the canister is gravity (air resistance can be ignored). A)How high is the rocket when the canister hits the launch pad, assuming that the rocket does not change its acceleration?

B)What total distance did the canister travel between its release and its crash onto the launch pad?

Answer 1

a) 919 mts

b) 392 mts

Step-by-step explanation:

In order to solve this, we will use the formulas of acceletared motion problems:

`(1)Y=Yo+Vo*t+(1)/(2)*a*t^2\\(2)Vf^2=Vo^2+2*a*y`

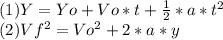
We are looking to obtain the initial velocity of the canister right after it was relased, we will use formula (2):

`Vf^2=(0)^2+2*(3.10)*(240)\\Vf=38.6 m/s`

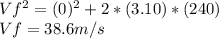
we need to calculate the time the canister takes to reach the ground, we will use formula (1):

`0-240m=38.6*t+(1)/(2)(-9.8m/s^2)*t^2\\\\-4.9*t^2+38.6*t+240=0\\t=11.9seconds`

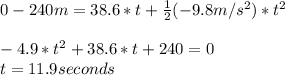
in order to know the new height of the rocket we have to use the formula (1) again:

`Y=240+38.6*(11.9)+(1)/(2)*(3.10)*(11.9)^2\\Y=919mts`

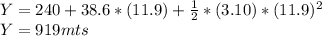
We can calulate the total distance the canister traveled before reach the ground by (2):

`(0)^2=(38.6)^2+2*(-9.8)*y\\Y=76m`

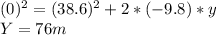
So the canister will go up another 76m, so the total distance will be:

`Yc=Yup+Ydown+240m\\Yc=76+76+240\\Yc=392 mts`