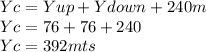Answer:
a) 919 mts
b) 392 mts
Step-by-step explanation:
In order to solve this, we will use the formulas of acceletared motion problems:
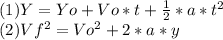
We are looking to obtain the initial velocity of the canister right after it was relased, we will use formula (2):
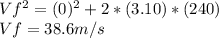
we need to calculate the time the canister takes to reach the ground, we will use formula (1):
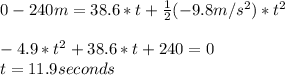
in order to know the new height of the rocket we have to use the formula (1) again:
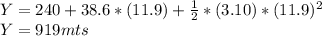
We can calulate the total distance the canister traveled before reach the ground by (2):
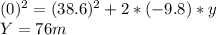
So the canister will go up another 76m, so the total distance will be: