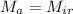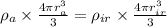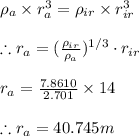Question

One cubic meter (1.00 m) of aluminum has a mass of 2.70 10 kg, and the same volume of iron has a mass of 7.8610'kg. Find the radus of a solid aluminum sphere that will balance a sod irn sphere o radu 14 squal-a balano rm

Answer 1

Radius of aluminium sphere which has same mass as of sphere of iron with radius 14 m is 40.745 meters.

Step-by-step explanation:

Let the radius of aluminium sphere be
`r_(a)`

From the relation between density, mass and volume we know that

`Mass=Density* volume...............(i)`

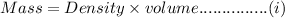
Applying equation 'i' separately to iron and aluminium sphere we get

`M_(a)=\rho _(a)* V_(a)`

`M_(ir)=\rho _(ir)* V_(ir)`

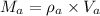
Equating the masses of iron and aluminium spheres we get

`M_(a)=M_(ir)`

`\rho _(a)* (4\pi r_a^3)/(3)=\rho _(ir)* (4\pi r_(ir)^3)/(3)`

`\rho _(a)* r_(a)^3=\rho _(ir)* r_(ir)^(3)\\\\\therefore r_(a)=((\rho _(ir))/(\rho _(a)))^(1/3)\cdot r_(ir)\\\\r_(a)=(7.8610)/(2.701)* 14\\\\\therefore r_a=40.745m`