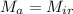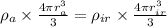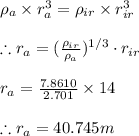Answer:
Radius of aluminium sphere which has same mass as of sphere of iron with radius 14 m is 40.745 meters.
Step-by-step explanation:
Let the radius of aluminium sphere be
From the relation between density, mass and volume we know that
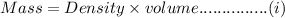
Applying equation 'i' separately to iron and aluminium sphere we get
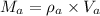
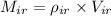
Equating the masses of iron and aluminium spheres we get