Question

Three point charges are arranged on a line. Charge q3 = +5.00 nC and is at the origin. Charge q2 = -2.00 nC and is at x = 5.00 cm . Charge q1 is at x = 2.50 cm .What is q1 (magnitude and sign) if the net force on q3 is zero?

Answer 1

q₁= +0.5nC

Step-by-step explanation:

Theory of electrical forces

Because the particle q3 is close to three other electrically charged particles, it will experience two electrical forces and the solution of the problem is of a vector nature.

To solve this problem we apply Coulomb's law:

Two point charges (q1, q2) separated by a distance (d) exert a mutual force (F) whose magnitude is determined by the following formula:

o solve this problem we apply Coulomb's law:

Two point charges (q₁, q₂) separated by a distance (d) exert a mutual force (F) whose magnitude is determined by the following formula:

F=K*q₁*q₂/d² Formula (1)

F: Electric force in Newtons (N)

K : Coulomb constant in N*m²/C²

q₁,q₂:Charges in Coulombs (C)

d: distance between the charges in meters

Data:

Equivalences

1nC= 10⁻⁹ C

1cm= 10⁻² m

Data

q₃=+5.00 nC =+5* 10⁻⁹ C

q₂= -2.00 nC =-2* 10⁻⁹ C

d₂= 5.00 cm= 5*10⁻² m

d₁= 2.50 cm= 2.5*10⁻² m

k = 8.99*10⁹ N*m²/C²

Calculation of magnitude and sign of q1

Fn₃=0 : net force on q3 equals zero

F₂₃:The force F₂₃ that exerts q₂ on q₃ is attractive because the charges have opposite signs,in direction +x.

F₁₃:The force F₂₃ that exerts q₂ on q₃ must go in the -x direction so that Fn₃ is zero, therefore q₁ must be positive and F₂₃ is repulsive.

We propose the algebraic sum of the forces on q₃

F₂₃ - F₁₃=0

`(k*q_(2) *q_(3) )/(d_(2)^(2)  ) -(k*q_(1) *q_(3) )/(d_(1)^(2)  )=0`

We eliminate k*q₃ of the equation

`(q_(1) )/(d_(1)^(2)  ) = (q_(2) )/(d_(2)^(2)  )`

`q_(1) =(q_(2) *d_(1) ^(2) )/(d_(2)^(2)  )`

`q_(1) =(2*10^(-9)*2.5^(2)*10^(-4)   )/(5^(2)*10^(-4)  )`

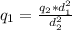
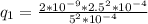
q₁= +0.5*10⁻⁹ C

q₁= +0.5nC