Answer:
2x - y - 7 = 0
Explanation:
Since the slope of parallel line are same.
So, we can easily use formula,
y - y₁ = m ( x ₋ x₁)
where, (x₁, y₁) = (8, 9)
and m is a slope of line passing through (x₁, y₁).
and since the slope of parallel lines are same, so here we use slope of parallel line for calculation.
and, Slope = m =
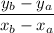
here, (xₐ, yₐ) = (2, 7)
and,
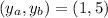
⇒ m =
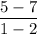
⇒ m = 2
Putting all values above formula. We get,
y - 9 = 2 ( x ₋ 8)
⇒ y - 9 = 2x - 16
⇒ 2x - y - 7 = 0
which is required equation.