Answer:
The total electric potential at mid way due to 'q' is

The net Electric field at midway due to 'q' is 0.
Solution:
According to the question, the separation between two parallel plates, plate A and plate B (say) = d
The electric potential at a distance d due to 'Q' is:
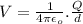
Now, for the Electric potential for the two plates A and B at midway between the plates due to 'q':
For plate A,
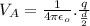
Similar is the case with plate B:
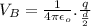
Since the electric potential is a scalar quantity, the net or total potential is given as the sum of the potential for the two plates:
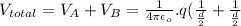
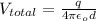
Now,
The Electric field due to charge Q at a distance is given by:
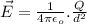
Now, if the charge q is mid way between the field, then distance is
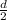 .
.
Electric Field at plate A,
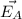 at midway due to charge q:
at midway due to charge q:
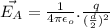
Similarly, for plate B:
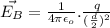
Both the fields for plate A and B are due to charge 'q' and as such will be equal in magnitude with direction of fields opposite to each other and hence cancels out making net Electric field zero.