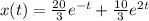Question

Exercise 0.2.9 : Verify that x = C 1 e − t + C 2 e 2 t is a solution to x ′′ − x ′ − 2 x = 0 . Find C 1 and C 2 to solve for the initial conditions x (0) = 10 and x ′ (0) = 0 .

Answer 1

Since 2 and -1 are eigenvalues of the differential equation,

`x(t) = c_(1)e^(-t) + c_(2)e^(2t)`

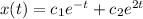
is a solution to the differential equation

-----------------------------------------------------------

The solution to the initial value problem is:

`x(t) = (20)/(3)e^(-t) +  (10)/(3)e^(2t)`

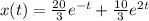
Explanation:

We have the following differential equation:

`x'' - x' - 2x = 0`

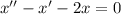
The first step is finding the eigenvalues for this differential equation, that is, finding the roots of the following second order equation:

`r^(2) - r - 2 = 0`

`\bigtriangleup = (-1)^(2) -4*1*(-2) = 1 + 8 = 9`

`r_(1) = (-(-1) + √(\bigtriangleup))/(2*1) = (1 + 3)/(2) = 2`

`r_(2) = (-(-1) - √(\bigtriangleup))/(2*1) = (1 - 3)/(2) = -1`

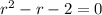
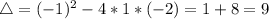
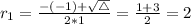
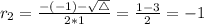
Since 2 and -1 are eigenvalues of the differential equation,

`x(t) = c_(1)e^(-t) + c_(2)e^(2t)`

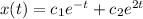
is a solution to the differential equation.

Solution of the initial value problem:

`x(t) = c_(1)e^(-t) + c_(2)e^(2t)`

`x(0) = 10`

`10 = c_(1)e^(-0) + c_(2)e^(2*0)`

`c_(1) + c_(2) = 10`

---------------------

`x'(t) = -c_(1)e^(-t) + 2c_(2)e^(2t)`

`x'(0) = 0`

`0 = -c_(1)e^(-0) + 2c_(2)e^(2*0)`

`-c_(1) + 2c_(2) = 0`

`c_(1) = 2c_(2)`

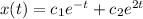
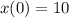
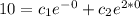
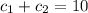
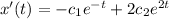
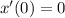
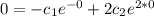
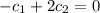
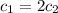
So, we have to solve the following system:

`c_(1) + c_(2) = 10`

`c_(1) = 2c_(2)`

`2c_(2) + c_(2) = 10`

`3c_(2) = 10`

`c_(2) = (10)/(3)`

`c_(1) = 2c_(2) = (20)/(3)`

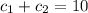
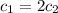
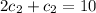
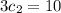
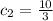
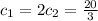
The solution to the initial value problem is:

`x(t) = (20)/(3)e^(-t) +  (10)/(3)e^(2t)`