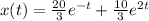Answer:
Since 2 and -1 are eigenvalues of the differential equation,
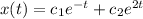
is a solution to the differential equation
-----------------------------------------------------------
The solution to the initial value problem is:
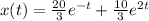
Explanation:
We have the following differential equation:
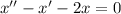
The first step is finding the eigenvalues for this differential equation, that is, finding the roots of the following second order equation:

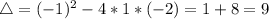

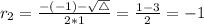
Since 2 and -1 are eigenvalues of the differential equation,
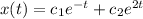
is a solution to the differential equation.
Solution of the initial value problem:
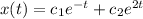
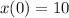
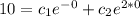
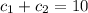
---------------------
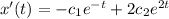
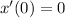
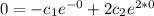
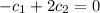
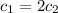
So, we have to solve the following system:
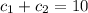
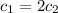
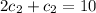


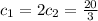
The solution to the initial value problem is: