Answer:
Explanation:
It is true that for any given odd integer, square of that integer will also be odd.
i.e if
 is and odd integer then
is and odd integer then
 is also odd.
is also odd.
In the given proof the expansion for
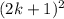 is incorrect.
is incorrect.
By definition we know,

∴

Now, we know
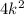 and
and
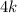 will be even values
will be even values
∴
 will be odd
will be odd
hence
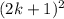 will be odd, which means
will be odd, which means
 will be odd.
will be odd.