Answer:
The magnitude of the resultant force is equal to 0.0216 N
The direction is along the negative y axis
Step-by-step explanation:
According to the exercise data:
q1 = 9x10^-6 C (0,1)
q2 = -9x10^-6 C (0,-1)
q = 7x10^6 C (6,0)
the distance between load q1 and load q will be equal to:
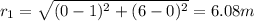
The same way to calculate the distance between q2 and q:

The force on q due to the load q1, is calculated with the following equation:
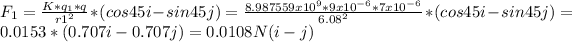
The same way to force F2:
F2 = (8.987559x10^9*-9x10^-6*7x10^-6))/(6.08^2)*(cos45i-sin45j) = 0.0108 N(i-j)
The resultant force:
F = F1 + F2 = 0.0108 N *(-2j) = - 0.0216 N j
The magnitude is equal to 0.0216 N
The direction is along the negative y axis