Question

A charge of 9 µC is on the y axis at 1 cm, and a second charge of −9 µC is on the y axis at −1 cm. Find the force on a charge of 7 µC on the x axis at x = 6 cm. The value of the Coulomb constant is 8.98755 × 10^9 N*m^2/C^2. Answer in n units of N.

Answer 1

The net force on X is Fx=75.4N

The net force on Y is FY=25.17N

Step-by-step explanation:

This is an electrostatic problem, we can calculate de force applying the formula:

`F=k*(Q*Q')/(r^2)\\where:\\k=coulomb constant\\r=distance\\Q=charge`

the force because of charge at 1cm on the X axis, will only have an X component of force, so:

`Fx1=8.98755*10^9*((9\µC)(7\µC))/((5*10^(-2)m)^2)\\Fx1=226.48N`

For the force because of the charge of the Y axis we have to find the distances usign pitagoras, and the angle:

`r=\sqrt{(-1*10^(-2)m)^2+(6*10^(-2)m)^2} \\r=6.08cm=0.0608m`

we can find the angle with:

`\alpha = arctg((1cm)/(6cm))=9.46^o`

We now can calculate the force of the X axis because of the second charge:

`Fx2=8.98755*10^9*((-9\µC)(7\µC))/((6.08*10^(-2)m)^2)*cos(9.46 )\\Fx2=-151.08N`

and for the Force on Y axis:

`Fy2=8.98755*10^9*((-9\µC)(7\µC))/((6.08*10^(-2)m)^2)*sin(9.46 )\\Fy2=-25.17N`

The net force on X axis is:

Fx=226.48N-151.08N=75.4N

Fy=-25.17N

Answer 2

The magnitude of the resultant force is equal to 0.0216 N

The direction is along the negative y axis

Step-by-step explanation:

According to the exercise data:

q1 = 9x10^-6 C (0,1)

q2 = -9x10^-6 C (0,-1)

q = 7x10^6 C (6,0)

the distance between load q1 and load q will be equal to:

`r_(1) = \sqrt{(0-1)^(2)+(6-0)^(2) }= 6.08 m`

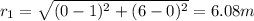
The same way to calculate the distance between q2 and q:

`r_(2) =\sqrt{(0-(-1))^(2)+(6-0)^(2) } =6.08 m`

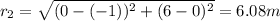
The force on q due to the load q1, is calculated with the following equation:

`F_(1)=(K*q_(1)*q )/(r1^(2) ) *(cos45i-sin45j)=(8.987559x10^(9)*9x10^(-6) *7x10^(-6) )/(6.08^(2) )*(cos45i-sin45j)=0.0153*(0.707i-0.707j)=0.0108N(i-j)`

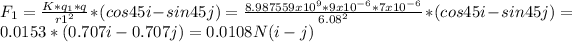
The same way to force F2:

F2 = (8.987559x10^9*-9x10^-6*7x10^-6))/(6.08^2)*(cos45i-sin45j) = 0.0108 N(i-j)

The resultant force:

F = F1 + F2 = 0.0108 N *(-2j) = - 0.0216 N j

The magnitude is equal to 0.0216 N

The direction is along the negative y axis