Answer:
The charge q₃ must be placed at X = +2.5 cm
Step-by-step explanation:
Conceptual analysis
The electric field at a point P due to a point charge is calculated as follows:
E = k*q/d²
E: Electric field in N/C
q: charge in Newtons (N)
k: electric constant in N*m²/C²
d: distance from charge q to point P in meters (m)
The electric field at a point P due to several point charges is the vector sum of the electric field due to individual charges.
Equivalences
1µC= 10⁻6 C
1cm= 10⁻² m
Data
k = 8.99*10⁹ N×m²/C²
q₁ =+3 µC =3*10⁻⁶ C
q₂ = -10 µC =-10*10⁻⁶ C
q₃= +6µC =+6*10⁻⁶ C
d₁ = 3cm =3×10⁻² m
d₂ = 4cm = 4×10⁻² m
Graphic attached
The attached graph shows the field due to the charges:
E₁:Field at point P due to charge q₁. As the charge is positive ,the field leaves the charge. The direction of E1 is (+ x).
E₂: Field at point P due to charge q₂. As the charge is positive ,the field leaves the charge. The direction of E1 is (+ x).
Problem development
E₃: Field at point P due to charge q₃. As the charge q₃ is positive, the field leaves the charge.
The direction of E₃ must be (- x) so that the electric field can be equal to zero at point P since E₁ and E₂ are positive, then, q₃must be located to the right of point P.
We make the algebraic sum of fields at point P due to the charges q1, q2, and q3:
E₁+E₂-E₃=0
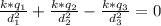
We eliminate k

We replace data
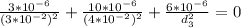
we eliminate 10⁻⁶

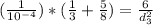
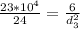

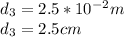
The charge q₃ must be placed at X = +2.5 cm