Question

A car is driven east for a distance of 50 km, then north for 28 km, and then in a direction 28° east of north for 21 km. Determine (a) the magnitude of the car's total displacement from its starting point and (b) the angle (from east) of the car's total displacement measured from its starting direction.

Answer 1

A ) displacement=75.69km

B) Angle
`= 28.92^o`

Step-by-step explanation:

This is a trigonometric problem:

in order to answer A and B , we first need to know the total displacement on east and north.

the tricky part is when the car goes to the direction northeast, but we know that:

`sin(\alpha )=(opposite)/(hypotenuse) \\where:\\opposite=north side\\hypotenuse=distance`

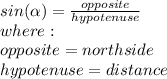
North'=9.86km

and we also know:

`cos(\alpha )=(adjacent)/(hypotenuse) \\where:\\adjacent=east side\\hypotenuse=distance`

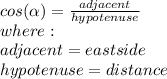
East'=18.54km

So know we have to total displacement

North=28km+North'=37.86km

East=50km+East'=68.54km

To calculate the total displacement, we have to find the hypotenuse, that is:

`Td=√(North^2+East^2) =75.69km`

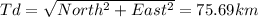
we can find the angle with:

`\alpha = arctg (\frac {North} {East}) \\\\ \alpha = arctg (\frac {37.86} {68.54})= 28.92^o`