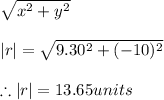Question

A vector A with an x-component of 6.00 and a y-component of -4.40 is added to a vector B with x-component 3.30 and a y-component of -5.60. What is the magnitude of the resultant vector? Use proper significant figures.

Answer 1

The magnitude of the resultant vector is 13.656 units.

Step-by-step explanation:

The vector A can be represented vectorially as

`\overrightarrow{r}_(a)=6.00\widehat{i}-4.40\widehat{j}`

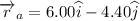
Similarly vector B can be represented vectorially as

`\overrightarrow{r}_(b)=3.30\widehat{i}-5.60\widehat{j}`

Thus upon adding the 2 vectors we get

`\overrightarrow{r}_(a)+\overrightarrow{r}_(b)=6.00\widehat{i}-4.40\widehat{j}+3.30\widehat{i}-5.60\widehat{j}\\\\=(6.00+3.30)\widehat{i}-(4.40+5.60)\widehat{j}\\\\=9.30\widehat{i}-10.00\widehat{j}`

Now the magnitude of the vector is given by:

|r|=
`\sqrt{x^(2)+y^(2)}\\\\|r|=\sqrt{9.30^(2)+(-10)^(2)}\\\\\therefore |r|=13.65units`