Question

Consider a business model in which two products, X and Y are produced. There are 160 pounds of material and 120 hours of labor available. It requires 4 pounds of material and 2 hours of labor to produce one unit of X. It requires 4 pounds of material and 6 units of labor to produce one unit of Y.

The profit for X is $35 and the profit for Y is $55. The business needs to know how many units of each product to produce to maximize resources and maximize profits. Express your answer in (x = , y = )

Maximize Z = 35x + 55y

subject to:

4x + 4y = 160

2x + 6y = 120

Answer 1

The maximum profit is $1600 at x=30 and y=10.

Explanation:

Let x be the number of units of product X.

y be the number of units of product Y.

The profit for X is $35 and the profit for Y is $55.

Maximize
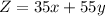`Z = 35x + 55y` ..... (1)

It requires 4 pounds of material and 2 hours of labor to produce one unit of X. It requires 4 pounds of material and 6 units of labor to produce one unit of Y.

Total material = 4x+4y

Total labor = 2x+6y

There are 160 pounds of material and 120 hours of labor available.

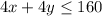`4x+4y\leq 160` .... (2)

`2x+6y\leq 120` ..... (3)

`x\geq 0,y\geq 0`

The related line of inequality (2) and (3) are solid line because the sign of equality "≤" contains all the point on line in the solution set.

Check the inequalities by (0,0).

`4(0)+4(0)\leq 160`

`0\leq 160`

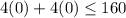
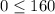
This statement is true.

`2x+6y\leq 120`

`2(0)+6(0)\leq 120`

`0\leq 120`

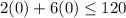
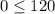
It means shaded region of both inequalities contain (0,0).

The extreme points of common shaded region are (0,0), (0,20), (40,0) and (30,10).

At (0,0),

`Z = 35(0) + 55(0)=0`

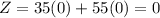
At (0,20),

`Z = 35(0) + 55(20)=110`

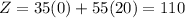
At (40,0),

`Z = 35(40) + 55(0)=140`

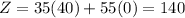
At (30,10),

`Z = 35(30) + 55(10)=1600`

Therefore the maximum profit is $1600 at x=30 and y=10.