Answer:
The maximum profit is $1600 at x=30 and y=10.
Explanation:
Let x be the number of units of product X.
y be the number of units of product Y.
The profit for X is $35 and the profit for Y is $55.
Maximize
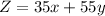 ..... (1)
..... (1)
It requires 4 pounds of material and 2 hours of labor to produce one unit of X. It requires 4 pounds of material and 6 units of labor to produce one unit of Y.
Total material = 4x+4y
Total labor = 2x+6y
There are 160 pounds of material and 120 hours of labor available.
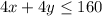 .... (2)
.... (2)
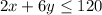 ..... (3)
..... (3)
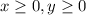
The related line of inequality (2) and (3) are solid line because the sign of equality "≤" contains all the point on line in the solution set.
Check the inequalities by (0,0).
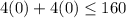
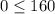
This statement is true.
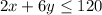
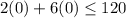
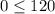
It means shaded region of both inequalities contain (0,0).
The extreme points of common shaded region are (0,0), (0,20), (40,0) and (30,10).
At (0,0),
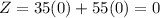
At (0,20),
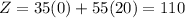
At (40,0),
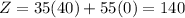
At (30,10),
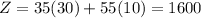
Therefore the maximum profit is $1600 at x=30 and y=10.