Answer:
a) 0°
b) 180°
c) 90°
Step-by-step explanation:
Hello!
To solve this question let a be the vector whose length is 15 m and b the vector of length 20 m
So:
|a | = 15
|b | = 20
Since we are looking for the angle between the vectors we need to calculate the length of the sum of the two vectors, this is:
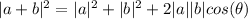
Now we replace the value of the lengths:
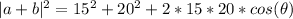
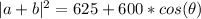 --- (1)
--- (1)
Now, if:
a) |a+b| = 35
First we can see that 20 + 15 = 35, so the angle must be 0, lets check this:



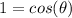
and :
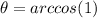
θ = 0
b) |a+b|=5
From eq 1 we got:
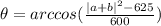 --- (2)
--- (2)
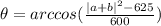
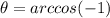
θ = π or θ = 180°
c) |a+b|=25
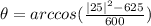
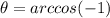
θ = π/2 or θ = 90°