Question

Consider two displacements, one of magnitude 15 m and another of magnitude 20 m. What angle between the directions of this two displacements give a resultant displacement of magnitude (a) 35 m, (b) 5 m, and (c) 25 m.

Answer 1

a) 0°

b) 180°

c) 90°

Step-by-step explanation:

Hello!

To solve this question let a be the vector whose length is 15 m and b the vector of length 20 m

So:

|a | = 15

|b | = 20

Since we are looking for the angle between the vectors we need to calculate the length of the sum of the two vectors, this is:

`|a+b|^(2) = |a|^(2) + |b|^(2) + 2 |a||b|cos(\theta)`

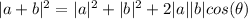
Now we replace the value of the lengths:

`|a+b|^(2) = 15^(2) + 20^(2) + 2*15*20*cos(\theta)`

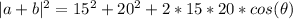
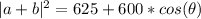`|a+b|^(2) = 625 + 600*cos(\theta)` --- (1)

Now, if:

a) |a+b| = 35

First we can see that 20 + 15 = 35, so the angle must be 0, lets check this:

`35^(2) = 625 + 600*cos(\theta)`

`1225 = 625 + 600*cos(\theta)`

`600 =  600*cos(\theta)`

`1= cos(\theta)`

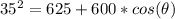
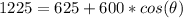
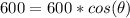
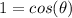
and :

`\theta = arccos(1)`

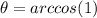
θ = 0

b) |a+b|=5

From eq 1 we got:

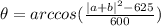`\theta = arccos((|a+b|^(2)-625)/(600))` --- (2)

`\theta = arccos((|a+b|^(2)-625)/(600))`

`\theta = arccos(-1)`

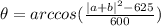
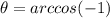
θ = π or θ = 180°

c) |a+b|=25

`\theta = arccos((|25|^(2)-625)/(600))`

`\theta = arccos(-1)`

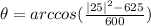
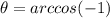
θ = π/2 or θ = 90°