Answer:
a) 21.8 mts
b) 10.2 seconds
c) 4.28 m/s
Step-by-step explanation:
Because the blimp is filled with helium, the acceleration won't be the gravity. We have to calculate the new acceleration:
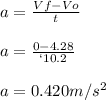
in order to obtain the height we have to use the formulas of accelerated motion problems:
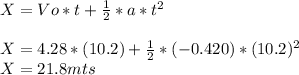
we can calculate the time with the same formula:
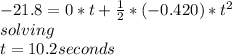
the velocity at the same height is given by:

the speed would be 4.28m/s because is a scalar value.