Answer: a) 0.1587 b) 0.0618
Explanation:
Let x be the random variable that represents the monthly demand for a product.
Given : The monthly demand for a product is normally distributed with mean = 700 and standard deviation = 200.
i.e.
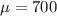 and
and
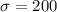
a) Using formula
 , the z-value corresponds to x= 900 will be :
, the z-value corresponds to x= 900 will be :
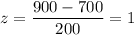
Now, by using the standard normal z-table , the probability demand will exceed 900 units in a month :-
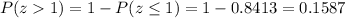
Hence, the probability demand will exceed 900 units in a month=0.1587
a) Using formula
 , the z-value corresponds to x= 392 will be :
, the z-value corresponds to x= 392 will be :
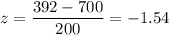
Now, by using the standard normal z-table , the probability demand will be less than 392 units in a month :-
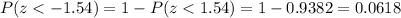
Hence, the probability demand will be less than 392 units in a month = 0.0618