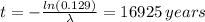Question

The bones of a saber-toothed tiger are found to have an activity per gram of carbon that is 12.9 % of what would be found in a similar live animal. How old are these bones?

Answer 1

The bones are 16925 years old

Step-by-step explanation:

We have to use the radioactive decay law and know that the half life of carbon-14 is
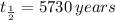`t_{(1)/(2)}=5730 \, years`. From this information we can know the decay rate of the carbon 14,

`\lambda=\frac{ln(2)}{t_{(1)/(2)}}=1.21* 10^(-4) s^(-1)`

Now to know the age of the bones we must directly use the radioactive decay law:

`N(t)=N_0e^(-\lambda t)=0.129N_0`

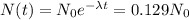
Where the rightmost part of the equation comes from the statement that the activity found is just 12.9% of the activity that would be found in a similar live animal. This means that the number of carbon-14 atoms is just 12.9% of what it was at the moment the saber-toothed tiger died.

Solving for t we have:

`t=-(ln(0.129))/(\lambda)=16925 \, years`