Explanation:
Consider the provided information.
For the condition statement
 or equivalent "If p then q"
or equivalent "If p then q"
- The rule for Converse is: Interchange the two statements.

- The rule for Inverse is: Negative both statements.
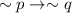
- The rule for Contrapositive is: Negative both statements and interchange them.
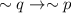
- The rule for Negation is: If p then q" the negation will be: p and not q.
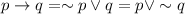
Part (A) If P is a square, then P is a rectangle.
Here p is "P is a square", and q is "Hill and P is a rectangle".
Negation: P is a square and P is not a rectangle.
Contrapositive: If P is not a rectangle then p is not a square.
Converse: If P is a rectangle then P is a square.
Inverse: If P is not a square then P is not a rectangle.
Part (B) If n is prime, then n is odd or n is 2
Here p is "n is prime", and q is "n is odd or n is 2".
Negation: n is prime and n is even and n is not 2.
Contrapositive: If n is not odd or n is not 2 then n is not prime.
Converse: If n is odd or n is 2 then n is prime.
Inverse: If n is not prime, then n is not odd or n is not 2.
Part (C) If 2 is a factor of n and 3 is a factor of n, then 6 is a factor of n.
Here p is "2 is a factor of n and 3 is a factor of n", and q is "6 is a factor of n".
Negation: 2 is a factor of n and 3 is a factor of n and 6 is not a factor of n.
Contrapositive: If 6 is not a factor of n then 2 is not a factor of n and 3 is not a factor of n.
Converse: If 6 is a factor of n then 2 is a factor of n and 3 is a factor of n.
Inverse: If 2 is not a factor of n and 3 is not a factor of n, then 6 is not a factor of n