Question

Communicate Mathematical Ideas Irrational numbers can never be precisely represented in decimal form. Why is this? 20 Unit1

Answer 1

An irrational number can never be represented precisely in decimal form.

Explanation:

A number can be precisely represented in decimal form if you can give a rule for the construction of its decimal part,

for example:

2.246973973973973... (an infinite tail of 973's repeated over and over)

7.35 (a tail of zeroes)

If this the case, then the number is a RATIONAL NUMBER, i.e, the QUOTIENT OF TWO INTEGERS.

Let's show this for the first example and then a way to show the general situation will arise naturally.

Suppose N = 2.246973973973...

You can always multiply by a suitable power of 10 until you get a number with only the repeated chain in the tail

for example:

1)
`N.10^3=2246.973973973...`

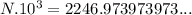
but also

2)
`N.10^6=2246973.973973...`

Subtracting 1) from 2) we get

`N.10^6-N.10^3=2246973.973973973... - 2246.973973973...`

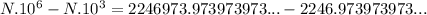
Now, the infinite tail disappears

`N.10^6-N.10^3=2246973 - 2246=226747`

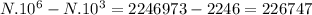
But

`N.10^6-N.10^3=N.(10^6-10^3)=N.(1000000-1000)=999000.N`

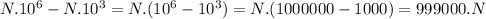
We have then

999000.N=226747

and

`N=(226747)/(999000)`

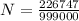
We do not need to simplify this fraction, because we only wanted to show that N is a quotient of two integers.

We arrive then to the following conclusion:

If an irrational number could be represented precisely in decimal form, then it would have to be the quotient of two integers, which is a contradiction.

So, an irrational number can never be represented precisely in decimal form.