Answer:
equation of plane, 5x+3y-z-36=0
Distance of point (2,2,2) from plane = 4.05 units
Explanation:
Given,
Plane passing through the point = (8, -2, 0)
Let's say,
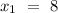
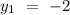

Plane perpendicular to the vector, a= 5i + 3j- k
Since, the vector is perpendicular to the plane, hence the equation of plane can be given by
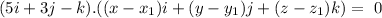
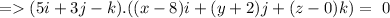
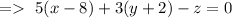
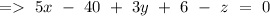
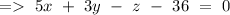
Hence, the equation of plane can be given by, 5x+3y-z-36=0
Now, we have to calculate the distance of the point O(2,2,2) from the plane 5x+3y-z-36=0
Let's say,
a= 5, b= 3, c= -1, d=-36
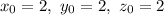
So, distance of a point from the plane can be given by,
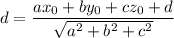
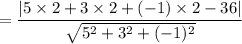
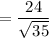
= 4.05 units
So, the distance of the point O(2,2,2) from the given plane will be 4.05 units.