Answer:
1.
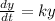
2.543.6
Explanation:
We are given that
y(0)=200
Let y be the number of bacteria at any time
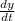 =Number of bacteria per unit time
=Number of bacteria per unit time
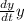
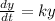
Where k=Proportionality constant
2.
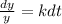 ,y'(0)=100
,y'(0)=100
Integrating on both sides then, we get

We have y(0)=200
Substitute the values then , we get
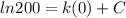

Substitute the value of C then we get
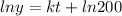
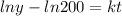
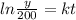
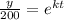
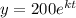
Differentiate w.r.t

Substitute the given condition then, we get
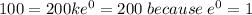
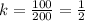
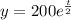
Substitute t=2
Then, we get
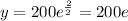
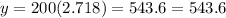
e=2.718
Hence, the number of bacteria after 2 hours=543.6