Answer:
The thermal efficiency of cycle is 42.6%.
Step-by-step explanation:
Given that
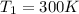
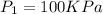
mass flow rate = 6 kg/s
Compression ratio = 7
Turbine inlet temperature = 1200 K
γ=1.4
We know that thermal efficiency of Brayton cycle given as
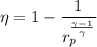
Now by putting the values
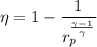
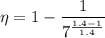
η=0.426
So the thermal efficiency of cycle is 42.6%.