Answer:
1) Height of oil in right limb = 67.31 cm
2) Height of water in the right limb = 16.83 cm
Step-by-step explanation:
The U-tube manometer is shown in the attached figure
Foe equilibrium The pressure at the bottom of the U tube should be same
Let the height of the water in the left limb of the manometer be
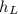
Thus the pressure at the bottom is found using the equation of pressure statics as
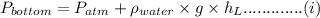
Similarly for the liquid in the right limb the pressure at the bottom is the sum of the oil column and the water column
Thus we can write

Equating the equations 'i' and 'ii' we get
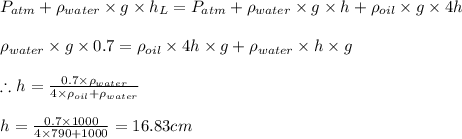
Thus the height of oil is
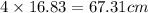 andthe height of water in the right limb is 16.83 cm.
andthe height of water in the right limb is 16.83 cm.