Question

Drug Ordered: Drug E, 1 mg/kg, SubQ, q12h for treatment of DVT. Drug Available: Drug E, 40 mg/0.4 mL syringe. Patient weight: 167 lb. a. How many kilograms does the patient weigh? (Round to the nearest tenth) ________ b. How many milligrams should the patient receive per day? (Round to the nearest tenth) ________ c. How many milliliters should the patient receive per dose? (Round to the nearest hundredth) ________

Answer 1

a) The patient weighs 75.15kg = 75.1kg, rounded to the nearest tenth.

b) The patient should 75.1mg a day of the drug.

c) The patient should receive 0.37mL per dose, rounded to the nearest hundreth.

Explanation:

These problems can be solved by direct rule of three, in which we have cross multiplication.

a. How many kilograms does the patient weigh?

The problem states that patient weighs 167lb. Each lb has 0.45kg. So:

1 lb - 0.45kg

167 lb - xkg

`x = 167*0.45`

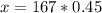
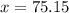`x = 75.15`kg

The patient weighs 75.15kg = 75.1kg, rounded to the nearest tenth.

b. How many milligrams should the patient receive per day?

The drug has 1mg/kg. The patient weighs 75.1kg. So

1 mg - 1 kg

x mg - 75.1kg

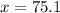`x = 75.1`mg

The patient should 75.1mg a day of the drug.

c. How many milliliters should the patient receive per dose?

The drug is SubQ, q12h. This means that the drug is administered twice a day, so there are 2 doses. 75.1mg of the drug are administered a day. so:

2 doses - 75.1mg

1 dose - xmg

`2x = 75.1`

`x = (75.1)/(2)`

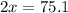
`x = 37.5` SubQ, q12h

For each dose, the patient should receive 37.5mg. Each 40mg of the drug has 0.4mL. So:

40mg - 0.4ml

37.5mg - xmL

`40x = 0.4*37.4`

`x = (0.4*37.4)/(40)`

`x = 0.374mL`

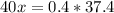
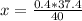
The patient should receive 0.37mL per dose, rounded to the nearest hundreth.