Explanation:
We will prove by contradiction. Assume that
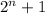 is an odd prime but n is not a power of 2. Then, there exists an odd prime number p such that
is an odd prime but n is not a power of 2. Then, there exists an odd prime number p such that
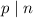 . Then, for some integer
. Then, for some integer
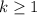 ,
,
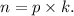
Therefore

Here we will use the formula for the sum of odd powers, which states that, for
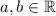 and an odd positive number
and an odd positive number
 ,
,
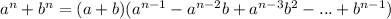
Applying this formula in 1) we obtain that
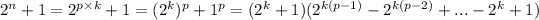 .
.
Then, as
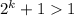 we have that
we have that
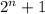 is not a prime number, which is a contradiction.
is not a prime number, which is a contradiction.
In conclusion, if
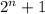 is an odd prime, then n must be a power of 2.
is an odd prime, then n must be a power of 2.