Question

A group of school children consist of 25 boys and 18 girls. how many ways are there:

1. to arrange the children in a row
2. To arrange the children in a row with all the boys next to each other
3. To arrange the children in a row with all the boys next to each other and all the girls next to each other.
4. To choose a chess team of 6 from the group if 1. Anyone can be chosen?
2. Exactly 2 girls must be chosen?
3. At least 2 boys must be chosen?

Answer 1

Explanation:

1. Number of boys in the group = 25

Number of girls in the group = 18

Total children = 25 + 18 = 43

Number of ways to arrange the children in a way = 43!

2. If we consider all the boys as an individual then number of ways children can be arranged = 19!

Number of ways boys can sit next to each other = 25!

So the number of ways can be arranged = 19!×25!

3. Number of ways boys can sit next to each other = 25!

Number of ways girls can sit next to each other = 19!

Then number of ways to arrange the children in a row with all boys next to each other and all the girls next to each other will be = 2 × 18! × 25!

4. 1. To choose a chess team if anyone can be chosen

=
`^(43)C_(6)`

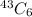
= 6096454

4. 2. Exactly 2 girls must be chosen then number of ways

=
`^(18)C_(2)* ^(25)C_(4)=1935450`

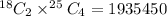
4. 3. At least two boys must be chosen

=
`^(25)C_(2)* ^(18)C_(4)+^(25)C_(3)* ^(18)C_(3)+^(25)C_(4)* ^(18)C_(2)+^(25)C_(5)* ^(18)C_(1)+^(25)C_(6)`

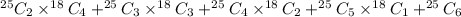
= 5863690