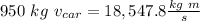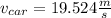Question

At the intersection of Texas Avenue and University Drive,

ablue, subcompact car with mass 950 kg traveling East on
universitycollides with a amrron pickup truck with mass 1900 kg
that istraveling north on Texas and ran a red light. The
twovehicles stick together as a result of the collision and, after
thecollision, the wreckage is sliding at 16.0 m/s in the
direction24.0 degrees east of north. Calculate the speed of
eachvehicle before the collision. the collision occurs during
aheavy rainstorm; you can ignore friction forces between
thevehicles and the wet road.

Answer 1

• The initial speed of the truck is 21.93 m/s, and the initial speed of the car is 19.524 m/s

Step-by-step explanation:

We can use conservation of momentum to find the initial velocities.

Taking the unit vector
`\hat{i}` pointing north and
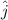`\hat{j}` pointing east, the final velocity will be

`\vec{V}_f = 16.0 (m)/(s) \ ( \ cos(24.0 \°) \ , \ sin (24.0 \°) \ )`

`\vec{V}_f = ( \ 14.617 (m)/(s) \ , \ 6.508 (m)/(s) \ )`

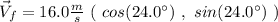
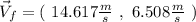
The final linear momentum will be:

`\vec{P}_f = (m_(car)+ m_(truck)) * V_f`

`\vec{P}_f = (950 \ kg \ + 1900 \ kg \ ) *  ( \ 14.617 (m)/(s) \ , \ 6.508 (m)/(s) \ )`

`\vec{P}_f = (2.850 \ kg \ ) *  ( \ 14.617 (m)/(s) \ , \ 6.508 (m)/(s) \ )`

`\vec{P}_f = ( \ 41,658.45 ( kg \ m)/(s) \ , \ 18,547.8 (kg \ m)/(s) \ )`

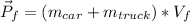
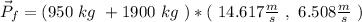
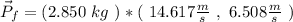
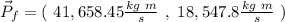
As there are not external forces, the total linear momentum must be constant.

So:

`\vec{P}_0= \vec{P}_f`

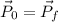
As initially the car is travelling east, and the truck is travelling north, the initial linear momentum must be

`\vec{P}_0= ( m_(truck) * v_(truck), m_(car)* v_(car) )`

so:

`\vec{P}_0= \vec{P}_f`

`( m_(truck) * v_(truck), m_(car)* v_(car) ) = ( \ 41,658.45 ( kg \ m)/(s) \ , \ 18,547.8 (kg \ m)/(s) \ )`

so

`\left \{ {{m_(truck) \ v_(truck) = 41,658.45 ( kg \ m)/(s)  } \atop {m_(car) \ v_(car)=18,547.8 (kg \ m)/(s) }} \right.`

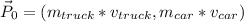
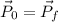
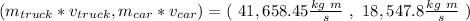
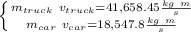
So, for the truck

`m_(truck) \ v_(truck) = 41,658.45 ( kg \ m)/(s)`

`1900 \ kg \ v_(truck) = 41,658.45 ( kg \ m)/(s)`

`v_(truck) = (41,658.45 ( kg \ m)/(s))/(1900 \ kg)`

`v_(truck) = (41,658.45 ( kg \ m)/(s))/(1900 \ kg)`

`v_(truck) = 21.93 (m)/(s)`

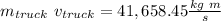
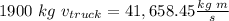
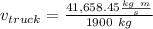
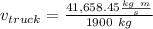
And, for the car

`950 \ kg \ v_(car)=18,547.8 (kg \ m)/(s)`

`v_(car)=(18,547.8 (kg \ m)/(s))/(950 \ kg)`

`v_(car)=19.524 (m)/(s)`