Answer:
13282.3 years
Step-by-step explanation:
The C-14 decays exponentially:
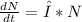
The solution for this equation is
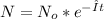
Where:
No = atom number of C-14 in t=0
N = atom number of C-14 now
I= radioactive decay constant
clearing t this equation we get:
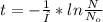
The term 1/I is called half-life and the value for C-14 is 8252 years.
N for this exercise is 0.2No
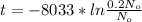
t = 13282.3 years