Question

Radioactivity of C-14 is used for dating of ancient artifacts. Archeologist determined that 20% of initial amount of C-14 has remained. Estimate the age of this artifact.

Answer 1

13282.3 years

Step-by-step explanation:

The C-14 decays exponentially:

`(dN)/(dt) =λ*N`

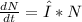
The solution for this equation is

`N= N_(o)*e^(- λt)`

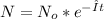
Where:

No = atom number of C-14 in t=0

N = atom number of C-14 now

I= radioactive decay constant

clearing t this equation we get:

`t=-(1)/( λ)*ln(N)/(N_(o))`

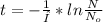
The term 1/I is called half-life and the value for C-14 is 8252 years.

N for this exercise is 0.2No

`t= -8033 * ln (0.2N_(o) )/(N_(o))`

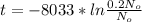
t = 13282.3 years