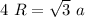Answer:
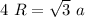
Step-by-step explanation:
Given that
Lattice constant = a
Radius of unit cell cell =R
Atom is in BCC structure.
In BCC unit cell (Body centered cube)
1.Eight atoms at eight corner of cube which have 1/8 part in each cube.
2.One complete atom at the body center of the cube
So the total number of atoms in the BCC
Z= 1/8 x 8 + 1 x 1
Z=2
In triangle ABD
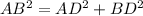
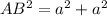
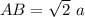
In triangle ABC
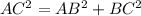
AC=4R
BC=a
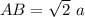
So
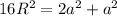
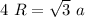
So the relationship between lattice constant and radius of unit cell