Question

A bar of 75 mm diameter is reduced to 73mm by a cutting tool while cutting orthogonally. If the mean length of the cut chip is 73.5 mm, find the cutting ratio. If the rake angle is 15 deg, what is the shear angle?

Answer 1

r=0.31

Ф=18.03°

Step-by-step explanation:

Given that

Diameter of bar before cutting = 75 mm

Diameter of bar after cutting = 73 mm

Mean diameter of bar d= (75+73)/2=74 mm

Mean length of uncut chip = πd

Mean length of uncut chip = π x 74 =232.45 mm

So cutting ratio r

`Cutting\ ratio=(Mean\ length\ of cut\ chip)/(Mean\ length\ of uncut\ chip)`

`r=(73.5)/(232.45)`

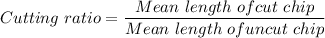
r=0.31

So the cutting ratio is 0.31.

As we know that shear angle given as

`tan\phi =(rcos\alpha )/(1-rsin\alpha )`

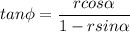
Now by putting the values

`tan\phi =(rcos\alpha )/(1-rsin\alpha )`

`tan\phi =(0.31cos15 )/(1-0.31sin15 )`\

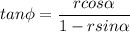
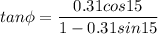Ф=18.03°

So the shear angle is 18.03°.