Question

The radius of Mercury (from the centerto just above the atmosphere)

is 2440km (2440103
m),and its mass is 0.31024
kg.An object is launched straight up from just above the atmosphere
ofMercury.
(a) What initial speed is needed so that when the object is farfrom
Mercury its final speed is2000 m/s?

Answer 1

u = 12962.11 m/s

Step-by-step explanation:

Given that,

The radius of mercury,
`r=2440\ km=2440* 10^3\ m`

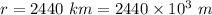
Mass of Mercury,
`M=3* 10^(24)\ kg`

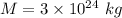
Final speed of the object, v = 2000 m/s

Let u is its initial speed when the object is far from Mercury. It can be calculated by applying the conservation of energy as :

Initial kinetic energy + gravitational potential energy = final kinetic energy

`(1)/(2)mu^2+(-(GmM)/(r))=(1)/(2)mv^2`

`(1)/(2)u^2+(-(GM)/(r))=(1)/(2)v^2`

`(1)/(2)u^2=(1)/(2)v^2+(GM)/(r)`

`u^2=2* ((1)/(2)v^2+(GM)/(r))`

`u^2=2* ((1)/(2)(2000)^2+(6.67* 10^(-11)* 3* 10^(24))/(2440* 10^3))`

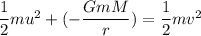
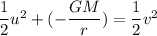
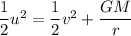
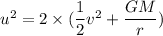
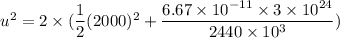
u = 12962.11 m/s

So, the initial speed of the object is 12962.11 kg. Hence, this is the required solution.