Question

A stone tied to the end of a string is whirled around in

avertical circle of radius R. Find the critical speed below
whichthe spring would become slack at the highest point.

Answer 1

`v=√(rg)`

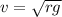
Step-by-step explanation:

radius of circle = R

Let T be the tension in the string.

At highest point A, the tension is equal to or more than zero, so that it completes the vertical circle. tension and weight is balanced by the centripetal force.

According to diagram,

`T + mg = (mv^(2))/(R)`

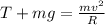
T ≥ 0

So,
`mg = (mv^(2))/(R)`

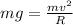
Where, v be the speed at the highest point, which is called the critical speed.

`v=√(rg)`

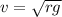
Thus, the critical speed at the highest point to complete the vertical circle is
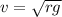`v=√(rg)`.

Answer 2

v = √rg.

Step-by-step explanation:

The Minimum speed of the stone that can have to the stone when it is rotated in a vertical circle is √rg.

Mathematical Proof ⇒

at the top point on the circle we have

T + mg = m v²/r

We know that minimum speed will be at the place when its tension will be zero.

∴ v² = rg

⇒ v = √rg.

So, the minimum speed or the critical speed is given as v = √rg.