Answer:
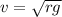
Step-by-step explanation:
radius of circle = R
Let T be the tension in the string.
At highest point A, the tension is equal to or more than zero, so that it completes the vertical circle. tension and weight is balanced by the centripetal force.
According to diagram,
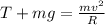
T ≥ 0
So,
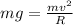
Where, v be the speed at the highest point, which is called the critical speed.
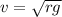
Thus, the critical speed at the highest point to complete the vertical circle is
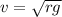 .
.