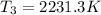Question

At the beginning of the compression process of an air-standard Otto cycle, p1 = 1 bar and T1 = 300 K. The compression ratio is 8.5 and the heat addition per unit mass of air is 1400 kJ/kg. Determine the maximum temperature of the cycle in Kelvin (input a number ONLY). Do not assume specific heats are constant. There is a ±5% tolerance.

Answer 1

Maximum temperature of the cycle is 2231.3 K

Step-by-step explanation:

See table (values there do not assume constant specific heat) and figure attached.

Assuming ideal gas behaviour, p1*v1 = p2*v2, rearranging p2/p1 = v1/v2

Data

`p_1 = 1 bar`

`T_1 = 300 K`

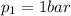
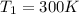
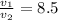`(v_1)/(v_2) = 8.5` (compression ratio)

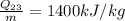`(Q_(23))/(m) = 1400 kJ/kg` (heat addition)

We can use the following relationship for air

`(v_1)/(v_2) = (v_(r1))/(v_(r2))`

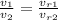
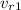`v_(r1)` is only function of temperature and can be taken from table. In this case:

`v_(r1) = 621.2`

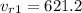
Rearranging previous equation

`v_(r2) = v_(r1) * (v_2)/(v_1)`

`v_(r2) = 621.2 * (1)/(8)`

`v_(r2) = 73.082`

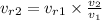
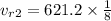
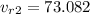
Interpolating from table

`u_2 = 503.06 kJ/kg`

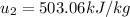
Energy balance in the process 2-3 gives

`(Q_(23))/(m) = u_3 - u_2`

`u_3 = (Q_(23))/(m) + u_2`

`u_3 = 1400 kJ/kg + 503.06 kJ/kg`

`u_3 = 1903.06 kJ/kg`

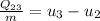
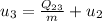
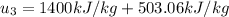
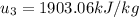
Interpolating from table

`T_3 = 2231.3 K`