Answer:
We are given that a manufacturer sells a product as $2 per unit.
Quantity = q units
So, Total revenue =
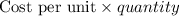
Total revenue =

So, the total revenue function is

Marginal revenue is the derivative of the revenue functions
So, Marginal revenue =
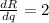
The marginal revenue function is 2
The constant marginal revenue function mean that the revenue earned by the addition of the output is constant.