Answer:
The flux of the electric field through the surface is 3.24\times10^{3}\ Nm^/C[/tex].
Step-by-step explanation:
Given that,
Area of cube = 48 cm²
Charge = 28.7 nC
We need to calculate the flux of the electric field through the surface
Using formula Gauss's law
The electric flux through any closed surface,
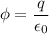
Where, q = charge
Put the value into the formula
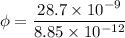
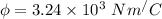
Hence, The flux of the electric field through the surface is 3.24\times10^{3}\ Nm^/C[/tex].