Answer: 208.3 s
Step-by-step explanation:
Hi!
You need to calculate the velocity of the boat relative to the shore, in each trip.
Relative velocities are transformed according to:

Let's take the upstram direction as positive. Water flows downstream, so it's velocity relative to shore is negative , -2 m/s
In the upstream trip, velocity of boat relative to water is positive: 10m/s. But in the downstream trip it is negatoive: -10m/s
In upstream trip we have:
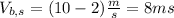
In dowstream we have:
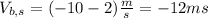
In both cases the distance travelled is 1000m. Then the time it takes the round trip is:
