Question

Show that 2 - sqrt(2) is irrational

Answer 1

This proof can be done by contradiction.

Let us assume that 2 - √2 is rational number.

So, by the definition of rational number, we can write it as

`2 -√(2) = (a)/(b)`

where a & b are any integer.

⇒
`√(2) = 2 - (a)/(b)`

Since, a and b are integers
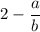`2 - (a)/(b)` is also rational.

and therefore √2 is rational number.

This contradicts the fact that √2 is irrational number.

Hence our assumption that 2 - √2 is rational number is false.

Therefore, 2 - √2 is irrational number.