Question

A 50kg boy runs at a speed of 10.0m/s and jumpsonto a cart

originally at rest. the cart, with the boy on it, thentakes off in
the same direction in which the boy was running. ifthe cart with
the boy has a velocity of 2.5m/s, what is the mass ofthe
cart?

Answer 1

Mass of the cart is 750 kg

Given:

Mass of the boy, m = 50 kg

Speed of the boy, v = 10.0 m/s

Final speed of the boy with the cart, v' = 2.5 m/s

Solution:

Initially the cart is at rest and since its on the ground, height, h = 0

Now, by the conservation of energy, mechanical energy before and after will remain conserved:

KE + PE = KE' + PE' (1)

where

KE = Initial Kinetic energy

KE' = Final Kinetic Energy

PE = Initial Potential Energy

PE' = Final Potential Energy

We know that:

Kinetic enrgy =
`(1)/(2)mv^(2)`

Potential energy = mgh

Since, potential energy will remain zero, thus we apply the conservation of Kinetic Energy only.

Let the mass of cart be M, thus the mass of the system, m' = 50 + M

Using eqn (1):

`(1)/(2)mv^(2) = (1)/(2)m'v^(2)`

`(1)/(2)* 50* 10^(2) = (1)/(2)(50 + M)* 2.5^(2)`

`5000 = 6.25(50 + M)`

M = 750 kg

Answer 2

the mass of the cart is 150 kg

Step-by-step explanation:

given,

mass of boy(m) = 50 kg

speed of boy (v)= 10 m/s

initial velocity of cart (u) = 0

final velocity of cart(V) = 2.5 m/s

mass of the cart(M) = ?

m v + M u = (m + M ) V......................(1)

50× 10 + 0 = (50 + M ) 2.5

M =
`(500)/(2.5) - 50`

M = 150 Kg

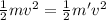
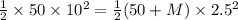
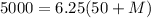
hence, the mass of the cart is 150 kg