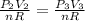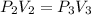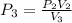Question

38.4 mol of krypton is in a rigid box of volume 64 cm^3 and is initially at temperature 512.88°C. The gas then undergoes isobaric heating to a temperature of 935.9°C. (a) What is the final volume of the gas?(in cm^3 ) (b) It is then isothermally compressed to a volume 29.3cm^3; what is its final pressure?(in Pa )

Answer 1

Final volumen first process
`V_(2) = 98,44 cm^(3)`

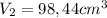
Final Pressure second process
`P_(3) = 1,317 * 10^(10) Pa`

Step-by-step explanation:

Using the Ideal Gases Law yoy have for pressure:

`P_(1) = (n_(1) R T_(1) )/(V_(1) )`

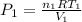
where:

P is the pressure, in Pa

n is the nuber of moles of gas

R is the universal gas constant: 8,314 J/mol K

T is the temperature in Kelvin

V is the volumen in cubic meters

Given that the amount of material is constant in the process:

`n_(1) = n_(2) = n`

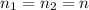
In an isobaric process the pressure is constant so:

`P_(1) = P_(2)`

`(n R T_(1) )/(V_(1) ) = (n R T_(2) )/(V_(2) )`

`(T_(1) )/(V_(1) ) = (T_(2) )/(V_(2) )`

`V_(2) = (T_(2) V_(1) )/(T_(1) )`

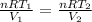
Replacing :
`T_(1) =786 K, T_(2) =1209 K, V_(1) = 64 cm^(3)`

`V_(2) = 98,44 cm^(3)`

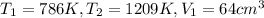
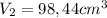
Replacing on the ideal gases formula the pressure at this piont is:

`P_(2) = 3,92 * 10^(9) Pa`

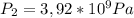
For Temperature the ideal gases formula is:

`T = (P V )/(n R )`

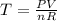
For the second process you have that
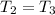`T_(2) = T_(3)` So:

`(P_(2) V_(2) )/(n R ) = (P_(3) V_(3) )/(n R )`

`P_(2) V_(2)  = P_(3) V_(3)`

`P_(3) = (P_(2) V_(2))/(V_(3))`

`P_(3) = 1,317 * 10^(10) Pa`